Summary
The double-elimination draw leading to a single-game final has become a standard of sorts at USCA tournaments, but the versions in common use can result in an unfair outcome. By reconfiguring the “losers” bracket, it is possible to construct a better and fairer draw of this type.
Background
The double-elimination draw has been a mainstay of USCA tournaments since the first National Championship in 1977. In those early days croquet courts in the US were few and far between. This left few practical options for how to format a tournament. Double-elimination was chosen as a way to guarantee every player at least two games without making the tournament too long.
Since then we have seen the development of new and larger tournament venues. Players now expect to play many games at a tournament, usually in a block (round robin) format followed by a playoff. With the block rounds guaranteeing each player a good number of games, single-elimination playoffs have become more acceptable. But at many tournaments, and certainly at the National Championship, double-elimination remains the playoff format of choice.
|
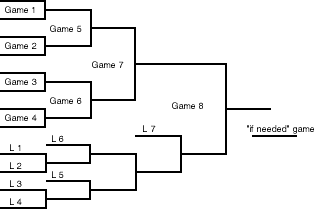
Diagram 1:
|
Double trouble
Except that somewhere along the way, an insidious innovation crept in: the “if needed” game was dropped. Apparently one reason for this is a compulsive desire to know exactly when the tournament will end. At any rate, the double-elimination playoff with single-game final has become the standard playoff format. Indeed, in seven years of tournament play I have never seen a double-elimination draw of the “classic” type, as shown in Diagram 1.
Obviously, a “double-elimination” draw that ends with a single-game final is not a true double-elimination draw. (I’ll call this type of format “pseudo-double-elimination”.) While, theoretically, the loss of the “if needed” game should make little difference to any player’s overall chances of winning the tournament (1), it can easily lead to a dubious outcome.
Referring to Diagram 1, if L7 wins his next game, he will immediately earn a rematch with the player who beat him in Game 7. If L7 then wins Game 8, these two players will have each beaten the other once. It is hardly logical to declare L7 the winner at this point, and yet that is exactly what happens in the pseudo-double-elimination format.
The usual reply to this criticism is to point out that L7 finishes with a better overall record than L8. While this is true (barely), it falls flat as a justification. One player reached Game 8 by means of a 3-0 record (i.e., three wins and no losses), the other with a 3-1 record. In other words, these two players achieved an equal position even though one of them had a patently inferior record. This is simply unfair.
The obvious solution is to restore the “if needed” game. But general opinion seems to be firmly in favor of the single-game final, even in light of its inherent unfairness.
The “face-off” draw
One variation that has been introduced in an effort to solve this disparity is the face-off draw. This is now the standard playoff format at the USCA National Championship.
The face-off simply divides the field in half, each half comprising a separate double-elimination ladder, complete with “if needed” games. (There is some crossover from one half to the other to avoid immediate rematches in the losers brackets.) The tournament final is a single-game playoff between the two ladder winners.
The problem with the face-off format is that while it decreases the likelihood of the unfairness described above, it doesn’t eliminate it. There is still the chance that one finalist will have a decidedly inferior record to the other (e.g., 4-1 vs. 4-0).
A better compromise
The pseudo-double-elimination format can be reasonably fair, so long as winning the losers bracket (the lower bracket) always requires more wins than winning the winners bracket (the upper bracket).
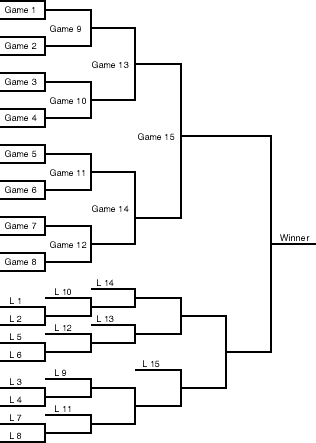
I devised a draw (2) that accomplishes this by a rearrangement of the final rounds of the losers bracket. Note Diagram 2:
|
Diagram 2:
|
Because L15 has to win two games to get to the final, this draw remedies the main unfairness of the standard pseudo-double-elimination draw.
The asymmetrical construction of the losers bracket has two interesting side effects. First, it shortens the entire draw by one round. The number of games remains the same, so this is an unqualified bonus. The Diagram 2 draw can be completed in seven rounds, versus eight rounds for either the standard pseudo-double-elimination draw or the face-off draw for the same number of players.
Second, all paths to the final that pass through the bottom bracket are of the same length. In the Diagram 2 draw, a player who loses a game at any stage and then goes on to win the final will have won six games. (In the standard draw, such a player might have won five, six, or seven games, depending on which game he lost.) This is also a benefit, because it means that within each bracket, all wins have equal value.
Of course, this losers bracket configuration can also be used in a true double-elimination draw, with some of the same advantages over the standard double-elimination draw. Not that I ever expect to see true double-elimination making a comeback as a USCA tournament format.
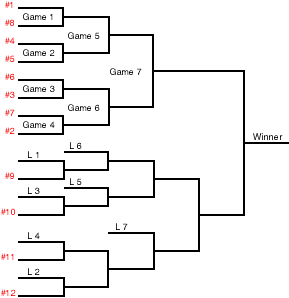
A limitation of my draw is that it doesn’t work with smaller numbers of players. Sixteen is the minimum if all players are to start from equal positions. Twelve-player versions are also possible, either by giving four players byes, or by starting four players directly in the bottom bracket. The latter is a more attractive format, and is shown in Diagram 3.
|
Diagram 3:
|
Conclusion
The “standard” form of the pseudo-double-elimination draw can easily result in an unfair outcome, and for this reason alone it should not be used. The face-off draw is somewhat better, but still suffers from the same basic problem (albeit to a lesser extent).
In terms of fairness, the best choice is to use a true double-elimination format. But the strong demand for formats with single-game finals calls for a different solution.
My modified draw eliminates the principal unfairness of the other pseudo-double-elimination draws. It is also more compact, requiring one less time period to complete. Either point alone is reason enough to use this draw in preference to the others.
Notes
- I made this determination after doing some computer analysis of various double-elimination formats. (This was a computer simulation using the Association Croquet World Ranking formula to predict outcomes, as suggested by Louis Nel’s tournament simulations.) I was actually expecting to find that doing away with the “if needed” game had a significant effect on outcome. I was then going to use that evidence to argue that pseudo-double-elimination formats are decidedly inferior to true double-elimination formats. But I found only a slight effect, and so have had to draw a different conclusion.
- I say that “I devised” this draw because I arrived at it independently. However, I expect that this is yet another example of re-inventing the wheel. Double-elimination is used in many different sports, and it seems likely enough that my discovery is not an original one.
Copyright notice
Copyright 2001–2008 by Jeff Soo.
You may make and distribute paper copies of this article, under the following conditions:
- each copy must include the complete text of the article, unmodified, including this copyright notice.
- the copies must be distributed free of charge.
Electronic distribution or re-publication is prohibited, unless permission has been granted by the author. However, you are
welcome to publish links to this article via email or WWW. Link to
http://ipsedixit.net/croquet/articles/formats/
8 December 2001